Quip:2-Bit Quantization of Large Language Models With Guarantees
1 Introduction
作者发现当权重和代理Hessian矩阵不相关时,量化过程更容易进行,因为权重的变化不会受到不同方向上的重要性差异的影响,从而减少了舍入误差的可能性,提高了量化的效率。具体来说,文章引入了不相干处理量化,包含两个步骤:1、自适应舍入过程。2、处理权重矩阵和海森矩阵不相干
2 Related Work
略
3 Quantization With Incoherence Processing: Adaptive Rounding Step
自适应舍入目标函数:
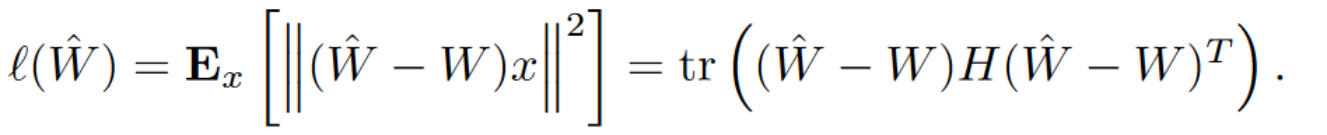
推导

3.1 LDLQ: An Optimal Adaptive Rounding Method
对于$k=1,2\dots n:$迭代更新${W}$:
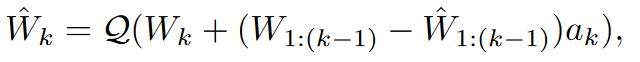
$W_k$表示第$k$列,$W_{1:(k-1)}$表示前$k-1$列,$\mathcal{Q}$表示对整数的最近舍入或者标准无偏摄入:$E[\mathcal{Q}(z)]=z$并且$a_k\in R^{k-1}$
每一次迭代,都会添加一个校正项,”校正”项是指在每一步迭代中,根据到目前为止的舍入结果与原始数据的差异(残差),计算出的一个线性函数。这个函数的作用是对当前列进行微调,以使得舍入结果更接近原始数据,或者满足特定的优化目标。具体地说,对于第 $k$ 列 $ \hat{W}_k $ ,修正项 $(W_{1:(k-1)} - \hat{W}_{1:(k-1)})a_k$是由前 $k-1$ 列舍入结果与原始数据的差异(即残差)乘以一个向量 $a_k$ 得到的。这个向量控制着对当前列的修正程度,可以看作是一个权重向量,用于调整前面列的残差对当前列的影响。
最终得到:
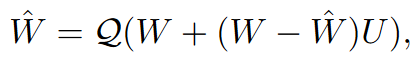
$U$是一个严格的上三角矩阵,他的列是向量$a_k$.
定义$\mathcal{Q}$的量化误差:
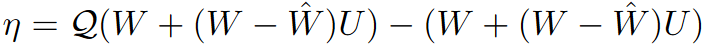
计算得到:
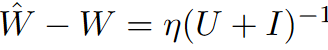
推理:
重写目标函数为:
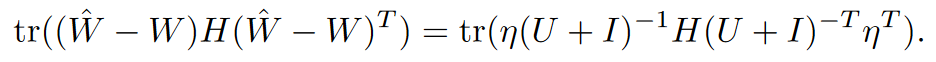
LDLQ方法:
对于上面的公式,如何确定$U$,根据重建的目标函数,令$U=\acute{U}$,对$H$进行LDL分解得到$\acute{U} $(它可以将一个对称正定矩阵A分解为一个下三角矩阵L、一个对角矩阵D和一个下三角矩阵L的转置的乘积,即$A = LDL^T$。其中,L是单位下三角矩阵(对角线元素为1,其它元素的下三角部分可能不为0,上三角部分全为0),D是对角线元素为正数的对角矩阵。:
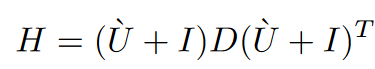
3.2 Deriving the Optimality of the LDLQ Adaptive Rounding Procedure
考虑最差和平均情况,令$\mathcal{A}$表示舍入方法,令$\mathcal{A}(W,H)$表示量化的权重,接下来定义最坏情况和平均情况:
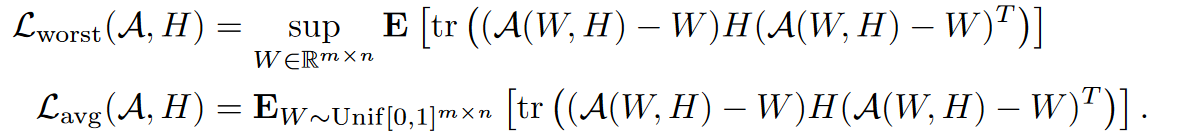
定理1:在将线性反馈 U规定为 H 的函数,并且舍入到整数时,LDLQ是最差情况和平均情况下最优的舍入方法。对于所有正半定 H,并且对于 $\mathcal{Q}$ 作为最近舍入或随机舍入:
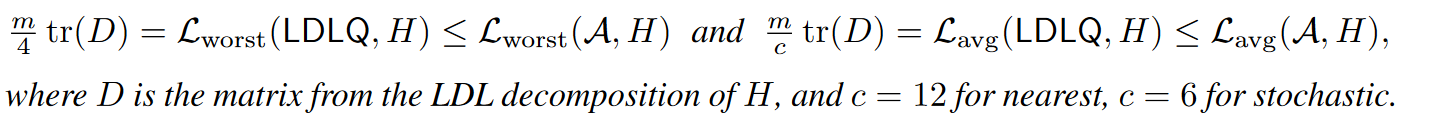
定理1证明:
令$X $为与舍入过程 $\mathcal{A}$ 相关的严格上三角矩阵,使得方程中的$ U ← X$,令$B \equiv (X+I)^{-1}(\acute{U}+I)$,损失为:
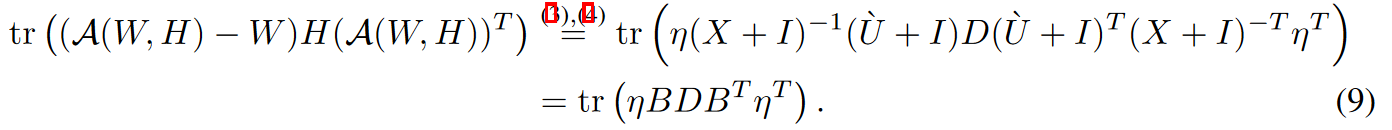
如果$U$是通过LDL分解得到的,则:
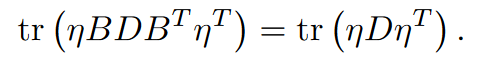
首先,考虑最坏情况损失,$L_{\text{worst}}$。目标是构造一个特别糟糕的情况,其中$\tilde{W}$的条目为$\frac{1}{2} \pm \epsilon$,因此当舍入到整数时,我们总是会有误差$\frac{1}{2}$。构造一个权重矩阵$\tilde{W} \in \mathbb{R}^{m \times n}$,使得每个条目满足,$ \tilde{W}_{ij} = \frac{1}{2} \pm \epsilon $
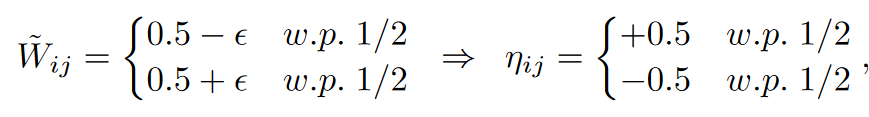
$\eta\in \R^{m,n}$,最坏情况的损失为,无论是随机还是最近舍入都有:
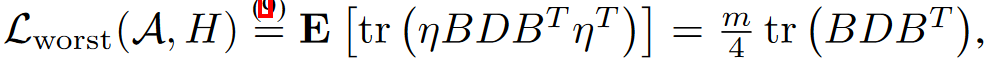
推导:
因此有:
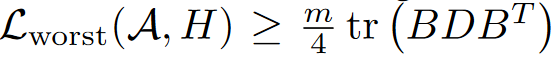
对于LDLQ,最坏的舍入误差也是0.5,因此:
$B \equiv (X+I)^{-1}(\acute{U}+I)$,$X+I$是单位上三角矩阵$\acute{U}+I$是单位下三角矩阵,当$B=I$时,$\frac{m}{4}\text{tr}(BDB^T)_{min}=\frac{m}{4}\text{tr}(D)$,
因此:
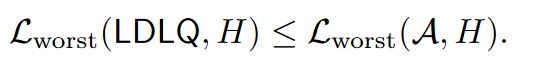
接下来证明平均损失:
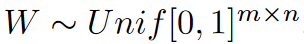
如果 $\mathcal{Q}$是最近舍入,则整个量化误差$\eta \sim Unif[-\frac{1}{2},\frac{1}{2}]$,所以:
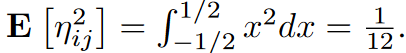
最终得到:
如果 $\mathcal{Q}$是随机舍入,则整个量化误差$\eta \sim Unif[-1,1]$,所以:
注意误差为$x$的概率为$(1-|x|)$,最终得到:
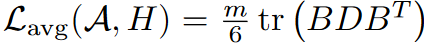
所以LDLQ量化的平均损失为:
最近舍入:
随机舍入:
所以有:
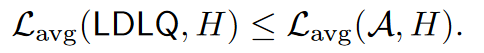
注意: $\mathcal{Q}$作为最接近的舍入实现了与随机舍入相同的最坏情况代理损失,但实现了更好的平均代理损失。
对于这些基线方法,它们与 LDLQ 的最优性差距由 tr (D) 与 tr (H) 决定.(公式4),从OPT125m到2.7B,实验表明,tr(D)/tr(H)<0.65,因此这个差距并非微不足道。
3.3 Incoherence: Optimality with a Spectral Bound
观察到H是低秩的:
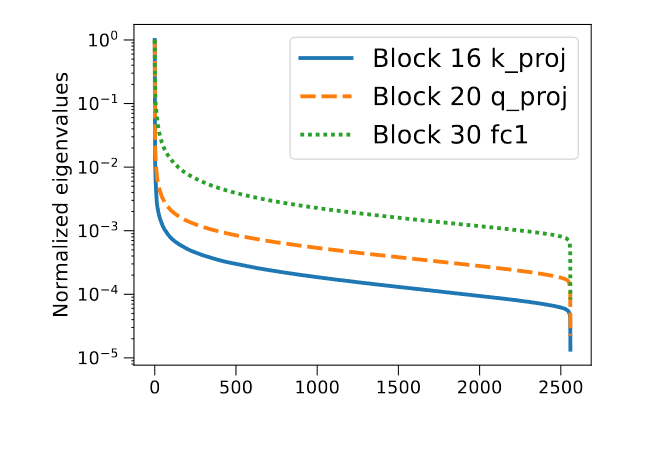
绝大多数的 H 矩阵的特征值中,有不到四分之一大于最大特征值的1%,基于对 H 低秩特性的这一观察,我们是否可以利用 H 的谱来限制 LDLQ 的行为,从而限制 tr(D) 的范围呢?
定义1:
定义“$\mu$-不一致”的概念,称对称的 Hessian 矩阵 $H$ 是 $\mu$-不一致的,如果它具有特征分解 $H = Q\Lambda Q^T$,使得对于所有的 $i$ 和 $j$,都满足 $|Q_{ij}| = \langle e_i, Qe_j \rangle \leq \frac{\mu}{\sqrt{n}}$。其中,$Q$ 是正交矩阵,$\Lambda$ 是对角矩阵,$e_i$ 是第 $i$ 个单位向量。这里的 $\langle \cdot, \cdot \rangle$ 表示向量的内积。进一步,通过推广,定义了“$\mu$-不一致”的概念,称权重矩阵 $W$ 是 $\mu$-不一致的,如果对于所有的 $i$ 和 $j$,都满足 $|W_{ij}| = \langle e_i, W e_j \rangle \leq \frac{\mu | W |_F}{\sqrt{mn}}$。其中,$| W |_F$ 表示权重矩阵 $W$ 的 Frobenius 范数。换句话说,对称的 Hessian 矩阵 $H$ 是 $\mu$-不一致的,意味着其特征向量 $Q$ 的每一列与单位向量之间的内积的绝对值都不超过 $\frac{\mu}{\sqrt{n}}$。而权重矩阵 $W$ 是 $\mu$-不一致的,则表示每个元素的绝对值与其对应的行向量和列向量的内积之积都不超过 $\frac{\mu | W |_F}{\sqrt{mn}}$ 与权重矩阵的 Frobenius 范数的乘积。
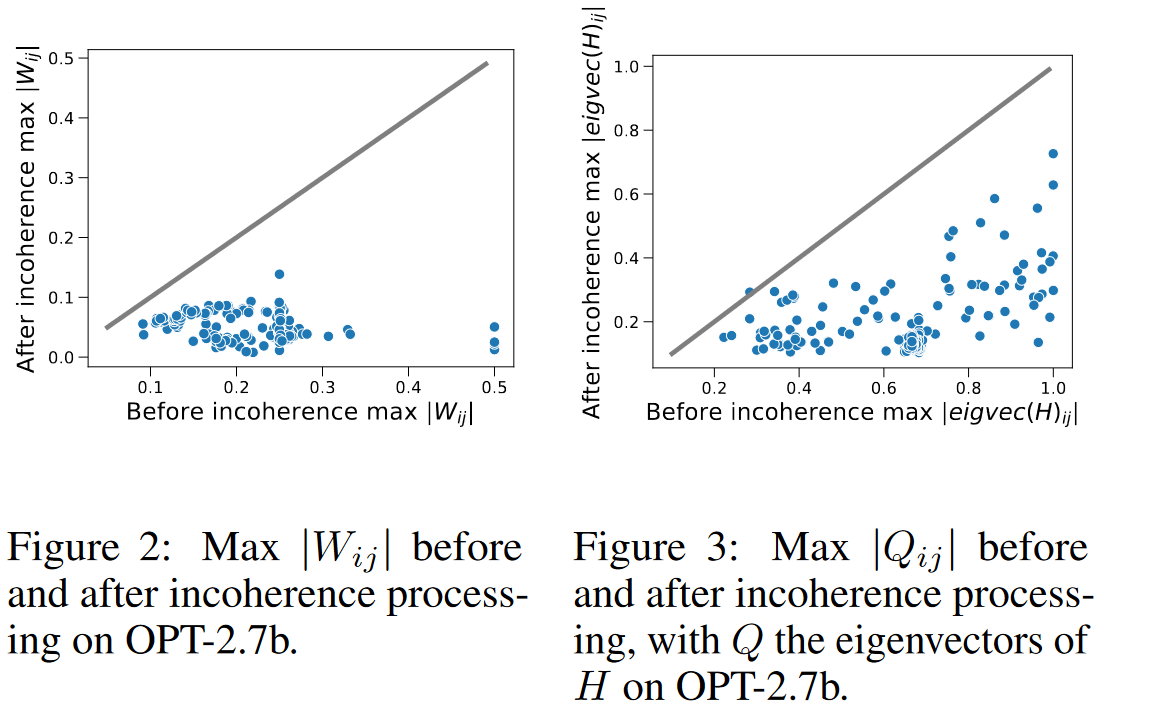
为什么在权重矩阵 $W$ 和 Hessian 矩阵 $H$ 中引入不一致性是有益的。首先指出,大多数的 $n \times n$ 矩阵具有与 $\mu = O(\sqrt{\log n}) = \tilde{O}(1)$ 的不一致性,这是因为一个随机正交矩阵的元素的平方大小集中在它们的平均值 $1/n$ 附近。因此,在权重矩阵 $W$ 中引入不一致性可以被视为一种异常值(outlier)减少的形式:对其元素的大小施加一个较小的边界意味着我们不需要那么大程度地对其进行缩放,以使其适应可表示的低精度数的有限范围。Figures 2 和 3 绘制了在 OPT-2.7b 的所有层中,在我们的不一致性处理前后的最大权重和 Hessian 特征向量的绝对值。参考线上的斜率为1。我们看到在我们的不一致性处理应用后,权重矩阵 $W$ 和 Hessian 矩阵 $H$ 更不一致($\mu 更小$)。虽然使 Hessian 矩阵 $H$ 不一致性不太直观,但其效用由以下引理所激发。
定理2:设 $H ∈ \mathbb{R}^{n \times n} $是一个 μ-不一致的半正定对称矩阵,其 $Cholesky$分解为 $H = (\acute{U} + I)D(\acute{U} + I)^T$,其中 $\acute{U} $是一个严格上三角矩阵,D 是一个(非负)对角矩阵,那么:
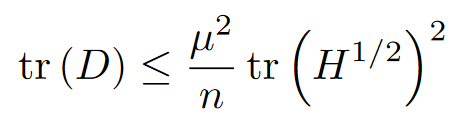
推理:不会
这是一项利用不一致性来获得仅依赖于矩阵 H 的谱的迹 $\text{tr}(D)$ 的界限的新颖结果.为了帮助解释这个结果,作者推导了普通最近邻和随机舍入的明确代理损失,然后将其与通过引理 2 获得的 LDLQ 方法进行比较。考虑矩阵 H的秩为 k,并且满足$ \mu^2 k < n$。根据柯西-施瓦茨不等式,我们有$ \text{tr}(H^{1/2})^2 \leq k \text{tr}(H)$,得到:
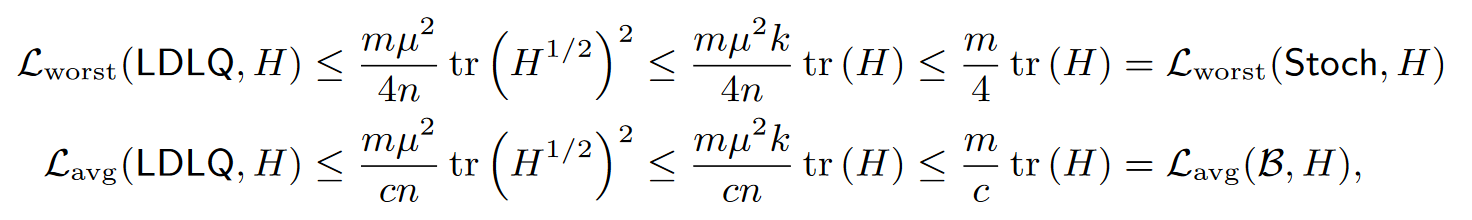
在这个情况下,$B \in \{Near, Stoch\}$,而 c如定理 1 中所示。这表明,对于足够低秩的 H,通过一个与$ \mu^2 k $有关的因子,LDLQ 在渐近意义下优于普通的最近邻和随机舍入。
没有不相干性:光谱界限没有改善。
定理4:
对于任何正半定的矩阵 H,如果考虑所有与 H具有相同谱的矩阵 $\tilde{H}$,那么在最坏情况下的损失上,LDLQ 方法实现的误差与随机舍入方法相同。
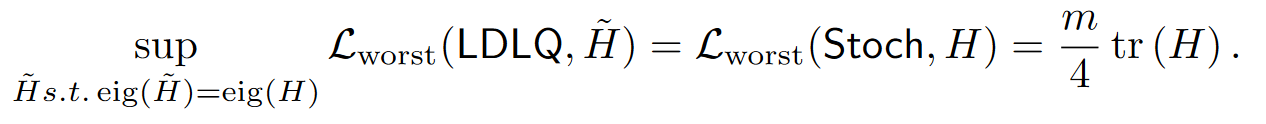
在平均情况下也是相同的误差:
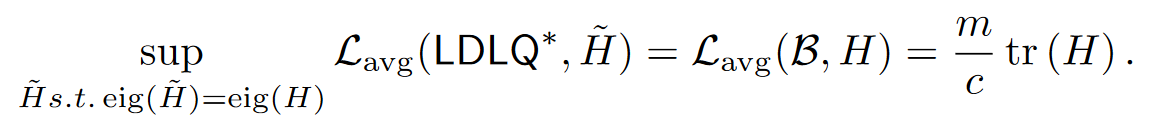
4 Quantization With Incoherence Processing: Incoherence Processing Step
使对称矩阵具有不一致性的一种直接方法是将其通过一个均匀随机正交矩阵进行共轭:这将导致其每个特征向量都是一个随机单位向量,其元素将集中在大小为 $n^{-1/2}$附近。
具体来说,假设 $U \in \mathbb{R}^{m \times m}$ 和 $V \in \mathbb{R}^{n \times n}$ 是两个随机正交矩阵。我们通过随机正交矩阵的乘法来确保权重和 Hessian 矩阵具有较高概率的不一致性,即:
$\tilde{H} \leftarrow V H V^T$
$\tilde{W} \leftarrow U W V^T$
这个转换保持了代理二次形式,因为
$\text{tr}(\tilde{W}\tilde{H}\tilde{W}^T) = \text{tr}((U W V^T)(V H V^T)(V W^T U^T)) = \text{tr}(W^T H W^T)$
4.1 Incoherence via Efficient Orthogonal Multiplication
在神经网络上运行推断任务而言,我们需要乘以权重矩阵 W,在这种情况下,需要生成并乘以n×n 的随机正交矩阵 U、V将会是不切实际的。解决方案:
即使用随机正交矩阵的分布,而不是单独生成随机正交矩阵进行乘法运算。该方法可以保证乘法运算的速度。首先,将 n 分解为 p和 q的乘积,其中 p 和 q大约等于 $\sqrt{n}$。然后,设置 $U = U_L \otimes U_R$,其中 $U_L$ 是从大小为 $p \times p$的正交矩阵集中随机采样,而 $U_R$是从大小为 $q \times q$ 的正交矩阵集中随机采样。对一个向量 $x \in \mathbb{R}^n$乘以矩阵 U 可以通过以下步骤实现:将向量重塑为一个大小为$ p \times q $的矩阵,在左侧乘以$ U_L$,在右侧乘以$ U_R^T$,然后将结果重塑回原始的向量形式。这个过程的时间复杂度为 $O(n(p+q)) = o(n^2)$。
定理5:
设 H是一个正半定矩阵,位于 $\mathbb{R}^{n \times n}$,W是一个矩阵,位于 $\mathbb{R}^{m \times n}$并假设 $m = p_1 \cdot p_2 \cdot \ldots \cdot p_k$ 以及 $n = q_1 \cdot q_2 \cdot \ldots \cdot q_k$。$ U_1, U_2, \ldots, U_k$和$ V_1, V_2, \ldots, V_k$是独立的随机正交矩阵,分别位于 $\mathbb{R}^{p_i \times p_i} $和$ \mathbb{R}^{q_i \times q_i}$。将 U 定义为Kronecker积 $U = U_1 \otimes U_2 \otimes \ldots \otimes U_K$,将 V定义为 $V = V_1 \otimes V_2 \otimes \ldots \otimes V_k$(实验中k=2),那么$VHV^T$是$\mu_H$不相关并且概率为$1-\delta$,$UWV^T$是$\mu_W$不相关并且概率为$1-\delta$:
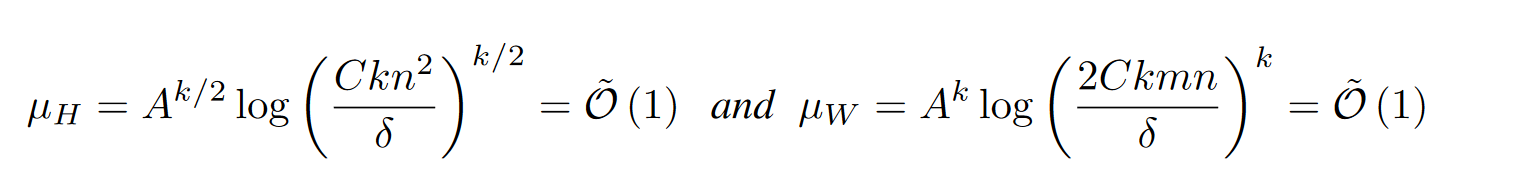
如果 A和 B都是正交矩阵,则它们的Kronecker积 $A \otimes B$也是正交矩阵。这是因为正交矩阵的乘积仍然是正交矩阵。Kronecker积的性质会保留矩阵的正交性.
算法:


第 4 行对角重新调整 W 和 H 的比例,以最小化 $\mathcal{L}(\hat {W}) ≈ tr (H) ∥W ∥^2_ F $,有效地权衡这些矩阵的频谱以找到最小值
受 W 不相干性的影响,第 6 行根据频谱 $∥W ∥^2_ F$ 计算量化范围,而不是典型的 $max_{i,j} |W_{ij}|$。
实验

总结
对目标函数进行变体之后发现,目标函数从原来的H的函数变为了D的函数,而且D比H小,如果H不相干,那么变体之后的损失小于变体之前的损失,于是对H进行了不相干处理。

